目前，在机器视觉和模式识别研究中，图像分割是一个关键的实验课题，其中，通过聚类对图像进行自动分割的方法普遍被应用在MR图像处理等方向。聚类分割算法就是将原始图像的所有像素分别进行标记，最终达到分割的效果。常用的聚类算法包括模糊C均值(FCM)、K-均值等。
最近十几年有许多基于统计的图像分割算法被提出，有限混合模型(Finite Mixture Model，FMM)[1]就是其中之一。当FMM模型中的概率分布为高斯概率分布时，则称其为高斯混合模型(Gaussian Mixture Model,GMM)[2]。它是利用最大期望(EM)算法[3]进行参数估计，进而利用统计概率对像素处理，但是高斯混合模型缺少对于邻近像素点之间关联性的研究，且对噪声十分敏感，以至于对存在噪声的图像进行分割后效果不佳。除此以外，GMM所用的EM算法中，M步有可能得不到先验分布的解析解，导致算法的复杂度和计算代价增加。
对此，本文构建了一种基于狄利克雷分布与参数分析的高斯混合模型(GMM-NI)，该模型对相邻像素之间的信息进行了处理。为了减少算法的复杂度，GMM-NI的先验概率被优先假设符合狄利克雷分布和狄利克雷定律。这样假设的优势在于GMM-NI保证了先验概率是正数且和为1，并且直接对模型的参数分别优化，即只要计算和更新均值、方差及一个狄利克雷参数就能得到目标参数。GMM-NI方法在参数优化上使用了梯度法，优化误差函数得到最小值。实验结果表明，GMM-NI在图像分割上比传统GMM算法更加可行且高效。
1高斯混合模型描述
高斯混合模型就是用高斯概率密度函数来刻画事物，从而得到数学模型。高斯混合模型被认为是描述灰度图像信息比较理想的模型之一[4]。 假设xi表示N个样本观测值，i=1,2,…,N，并且都服从独立同分布，把它们再对应为一幅灰度图像中第i个像素，则定义它们都服从K类的有限高斯混合分布，分别标记为(Ω1,Ω2,…,ΩK)。xi的密度函数为
(1)
其中：Π={πj},j=1,2,…,K为像素xi属于Ωj类的先验概率的集合，它符合以下约束条件：
(2)
G(xi|Θj)是服从均值为μj、方差为
的高斯分布。
(3)
这样X=(x1,x2,…,xN)的联合条件概率密度表示为
(4)
传统的GMM进行参数估计时，往往使用最大似然估计法。最大似然法使像素在计算概率密度时得到概率值最大。由于概率值一般都很小，结果可能得到极小值，使浮点数下溢，所以对式(4)取对数来优化算式，从而GMM的最大对数似然函数记为
(5)
2基于邻域信息的高斯混合模型及其算法描述
2.1狄利克雷分布与狄利克雷参数
本文使用基于狄利克雷分布和狄利克雷定律[5-6]的模型对邻近像素进行处理。首先定义一个概率标签：
p(zi|ξi)=
p(zi|ξi)p(ξi|ai)dξi
(6)
其中zi=(zi1,zi2,…,ziK)为对于第i个像素的离散概率标签。
(7)
ξi=(ξi1,ξi2,…,ξiK),i=1,2,…,N为狄利克雷参数，满足以下条件：
(8)
ai=(ai1,ai2,…,aiK)是狄利克雷参数ξi的向量，其元素aij≥0，i=1,2,…,N，且函数p(zi|ξi)可以写成多项式形式[7]：
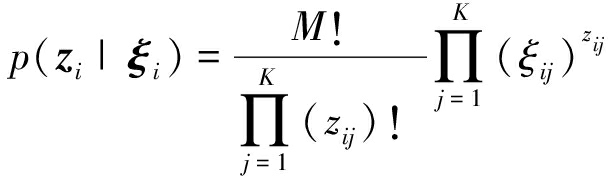
(9)
则推导出概率密度函数p(ξi|ai)如下：
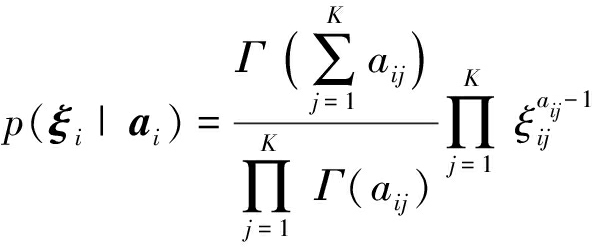
(10)
为了结合邻域信息，将狄利克雷参数aij定义为
(11)
其中，
是当前迭代的后验概率，表示为
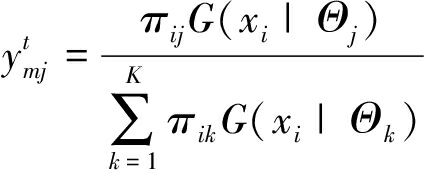
(12)
其中G(xi|Θj)是高斯概率密度函数
式(11)中括号内的部分可以看作是一个线性滤波器，即理解为把一个像素及其周围的像素取它们的均值乘以系数β来代替该范围的像素值，起到平滑噪声的作用。该滤波的模板是以xi为中心的3×3或者5×5的像素，Ni为窗口中像素数量的总和。根据式(9)和式(10)，将式(6)的概率标签重新写成为
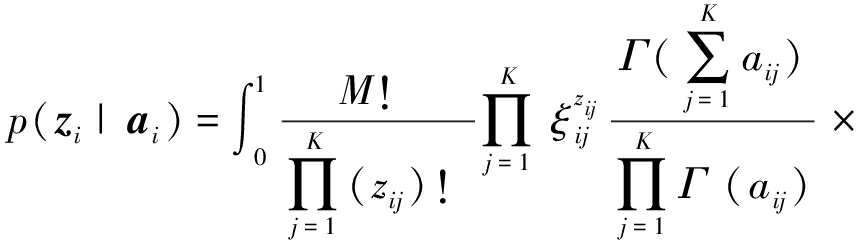
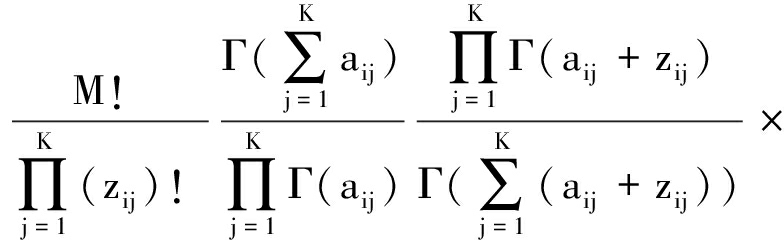
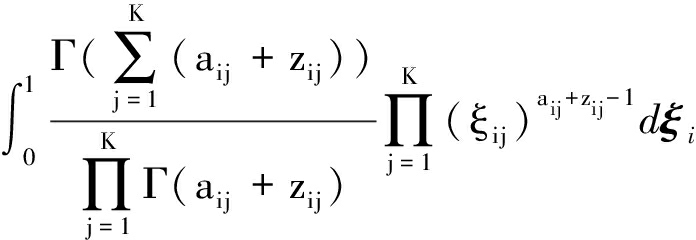
(13)
已知给定一个狄利克雷分布，根据性质，它的概率密度函数总满足以下条件：
p(ξi|ai)dξi=
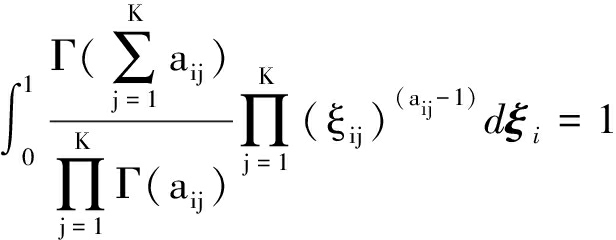
(14)
把式(11)和式(14)带入式(13)，可以得到概率标签：
p(zi|ai)=
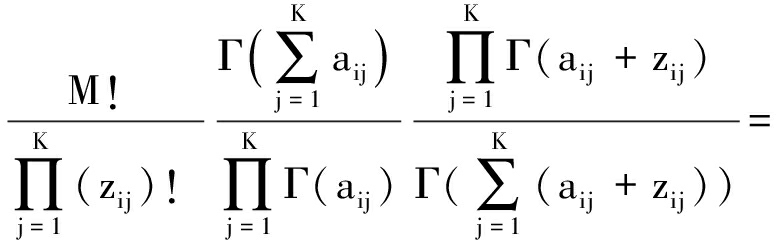
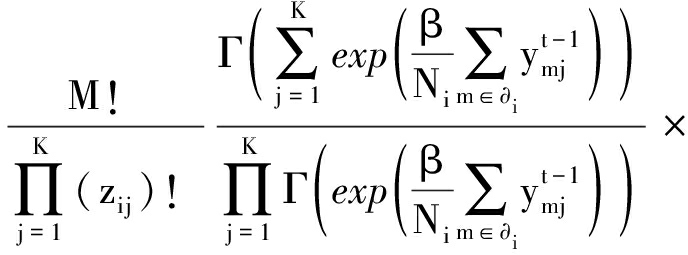
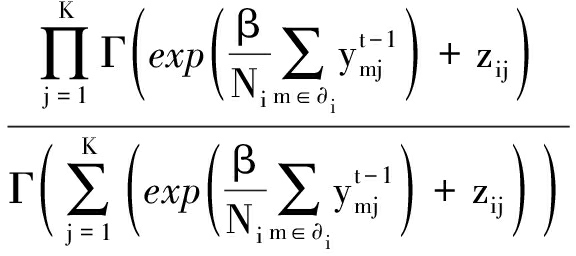
(15)
在上述的狄利克雷模型中，算法只需处理均值、方差和参数β即可。该狄利克雷模型是把邻近像素间的邻域信息以线性滤波的形式包括在狄利克雷参数中(即式(11))，然后把式(7)中的离散标签条件代入式(15)。同时令M=1，zij=1,又由于伽马函数有性质Γ(t+1)=tΓ(t) ，则得到像素xi属于某一类的先验概率πij：
πij=p(zij=1|ai)=
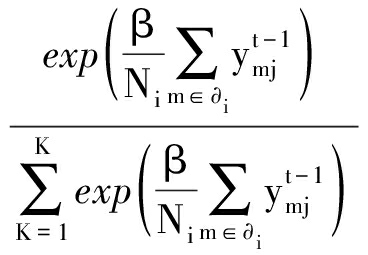
(16)
则对数似然函数表示为
(17)
其中，参数集Ξ={μj,σj,βj} ，G(xi|Θj)为高斯分布概率密度函数(式(3))，πij为先验概率(式(16))。由于对数函数是单调递增的，所以取其负值进行计算，即
J(Ξ)=-L(Ξ)
(18)
这里采用差分形式来表示一个误差函数：
J(Ξt+1)-J(Ξt)=
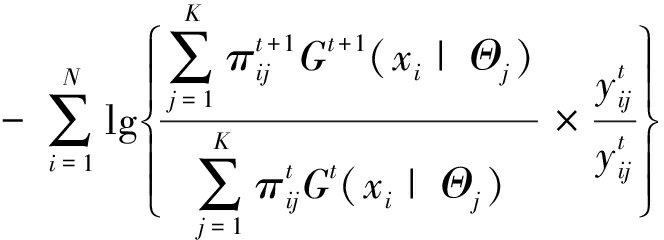
(19)
由于
且
使用Jensen不等式，式(19)可以重写为
J(Ξt+1)-J(Ξt)≤
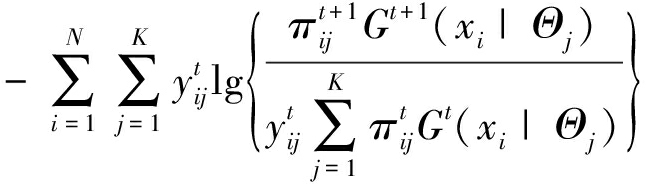
(20)
要最大化t+1次迭代后的对数似然函数，所以对式(20)进行简化，使其等价于最小化误差函数E(Ξ)，得到
(21)
由于上述最小误差函数用EM算法来估计参数时算法的复杂性增加，所以本文采用梯度下降法对最小误差函数进行求解。
图1 4种算法对图像的分割结果(聚类数为3)
Fig.1 Segmentation results of four algorithms (label 3)
2.2梯度法
梯度法的基本迭代表达式为
xk+1=xk+λkdk
(22)
每次迭代的搜索方向dk取为目标函数的负梯度方向，即
(23)
最速下降法计算量小，而且对初始点不敏感，所以本文的最小误差函数求解问题是利用最速下降法对参数集Ξ={μ，σ，β}中每一个变量分别进行计算，其迭代表达式为
(24)
其中对参数集Ξold的{μ,σ,β}分别计算，即对式(21)求导。
对μ求导
(25)
对σ求导
(26)
对β求导
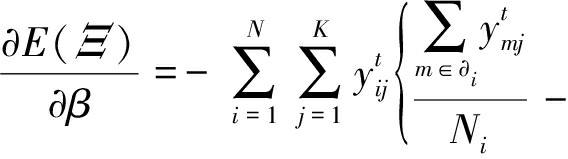
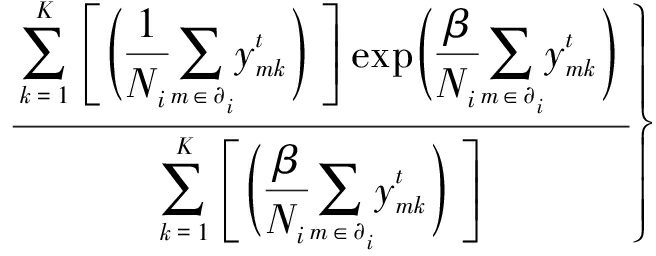
(27)
2.3算法流程
(1) 初始化参数。初始化均值μ、方差σ2以及参数β，将参数带入式(12)求得后验概率
每一类的μ、σ2可以由K-均值算法简单初始化。β设为20，学习率η设为10-6。
(2) 用式(16)计算先验概率πij，然后通过式(12)计算后验概率
(3) 分别通过式(25)、(26)、(27)求出参数μ、σ、β的下降梯度变化量
然后使用式(24)对参数集进行更新。
(4) 检查误差函数的收敛性。如果不满足条件，则使Ξnew=Ξold，返回步骤(2)。
(5) 在算法收敛条件下，对每一类的后验概率yi计算，取出类间概率最大值，并给每个像素点分配该类的标签，则分割算法结束。
3实验结果与分析
实验环境为Matlab2016a，实验样本取自Berkeley数据库和IBSR医学影像数据库。将本文算法与FCM、K-均值以及基于概率统计的GMM算法进行对比。
图1示出了4种算法对聚类数为3的图像进行分割的结果。可以看出本文方法(GMM-NI)相对于FCM、K-均值、GMM的滤波平滑效果比较明显，而且分割的效果也较好。
图2示出了4种算法对聚类数为4的图像进行分割的结果。可以看到，FCM、K-均值两种方法对于背景的滤除能力很差，GMM和本文算法都考虑了相邻像素间的关系，但本文算法对背景的滤除效果更加有效。由于本文算法引入了较强的滤波模板，对细节进行了平滑处理，所以效果更好。
医学图像经常需要通过算法分割得到较清晰的研究图像，大多使用无监督混合模型的方法对大脑MRI进行分割[8-9]。由于医学图像为灰度图像，且在采集时往往带有一定噪声，所以本文算法更为适用。
图2 4种方法对图像的分割结果(聚类数为4)
Fig.2 Segmentation results of four algorithms (label 4)
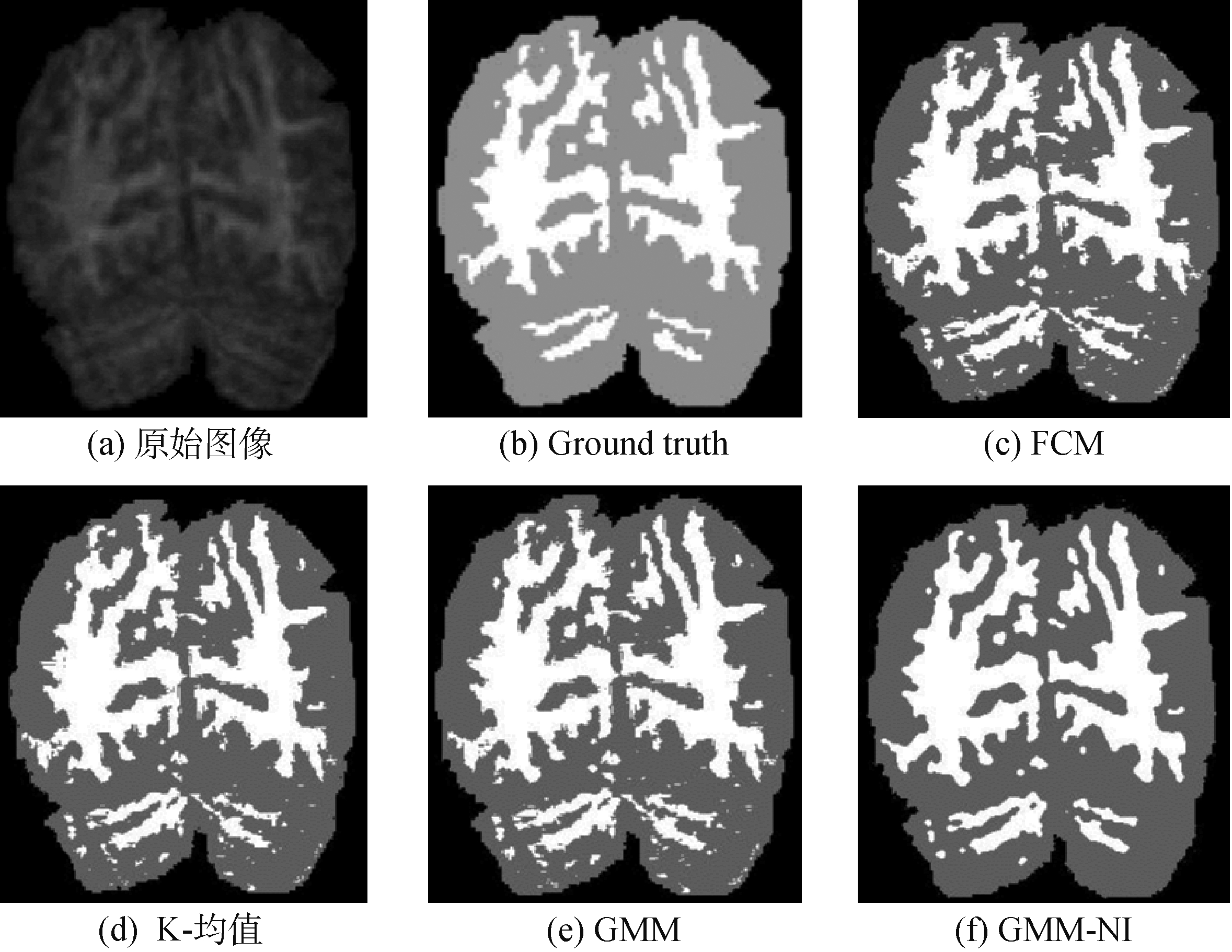
图3 对大脑MR图像的分割结果(聚类数为3，水平面)
Fig.3 Segmentation results of brain MR images (label 3, horizontal planes)
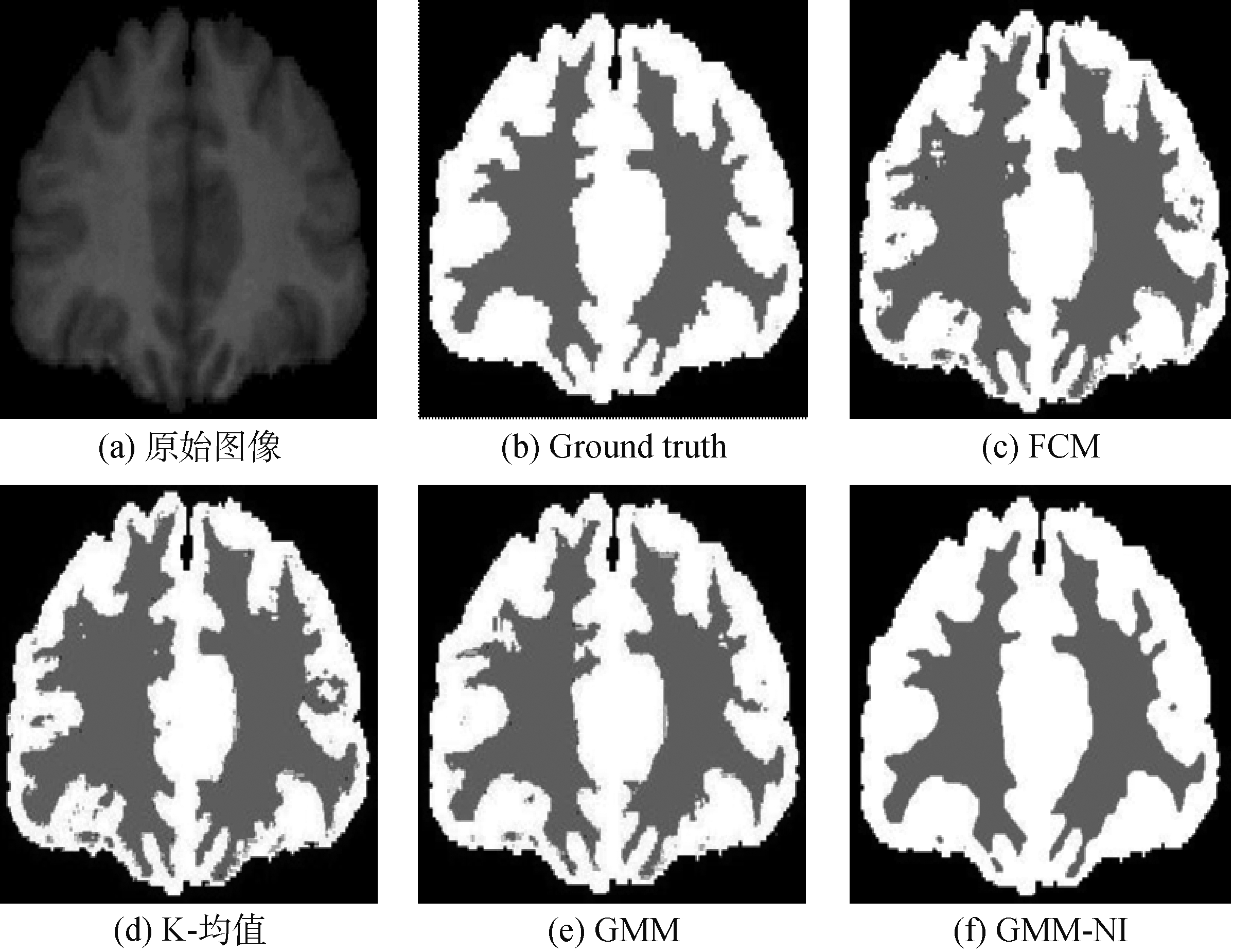
图4 对大脑MR图像的分割结果(聚类数为3，冠状面)
Fig.4 Segmentation results of brain MR images (label 3, coronal)
本文算法与其他传统分割算法对医学低噪图像的分割效果如图3(c)～(f)和图4(c)～(f)所示。从给出的Groundtruth 和分割后的图可以看出，基于邻域信息的高斯混合模型分割能起到显著的平滑滤波去除伪影的效果，而且分割的效果也相对清晰明显。
为了定量地分析本文算法的有效性，对图3、图4及其他几幅大脑MR图像进行分割。一般采用MCR[10-11]算法和Dice算法[12]对医学图像误差进行评估，本文根据MCR算法对分割的错误率(MCR)进行计算，结果如表1所示。
(28)
对带有噪声的MR图像进行聚类实验，以验证算法的分割性能。同样使用了图3中的大脑图像作为实验样本，图5示出了带有均值为0、方差为0.01的高斯噪声的大脑图像的分割结果。图6示出了带有1%的椒盐噪声的大脑图像的分割结果。
表1 4种算法对于4幅不同的大脑MRI图像分割错误率
Table 1Segmentation error rate of four algorithms in different brain images
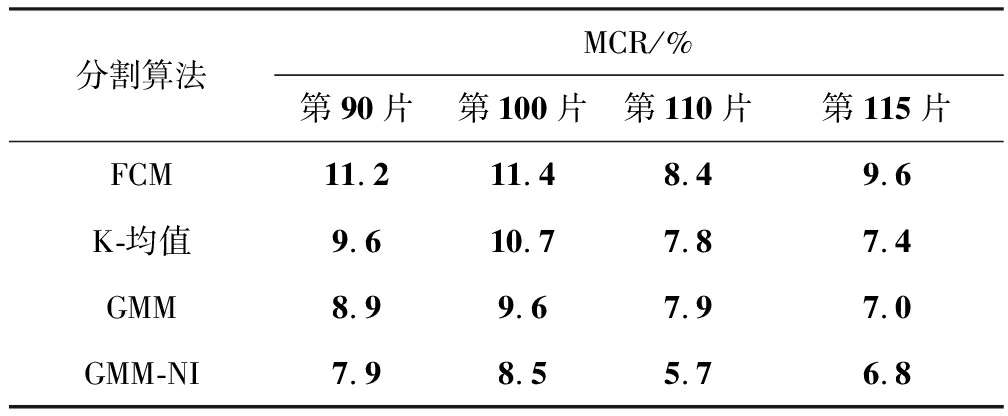
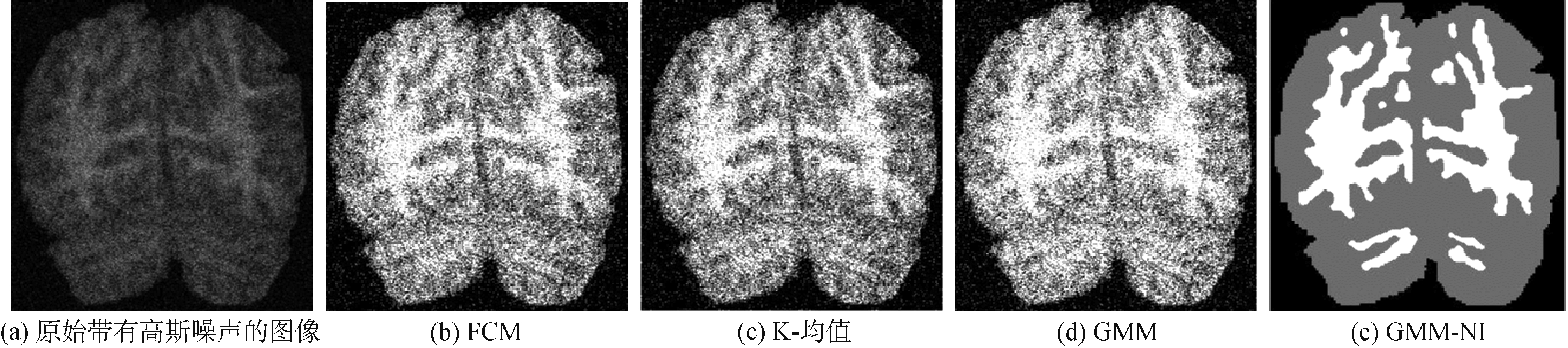
图5 4种算法对含有高斯噪声的大脑图片的分割结果
Fig.5 Segmentation results on Gaussian noise images
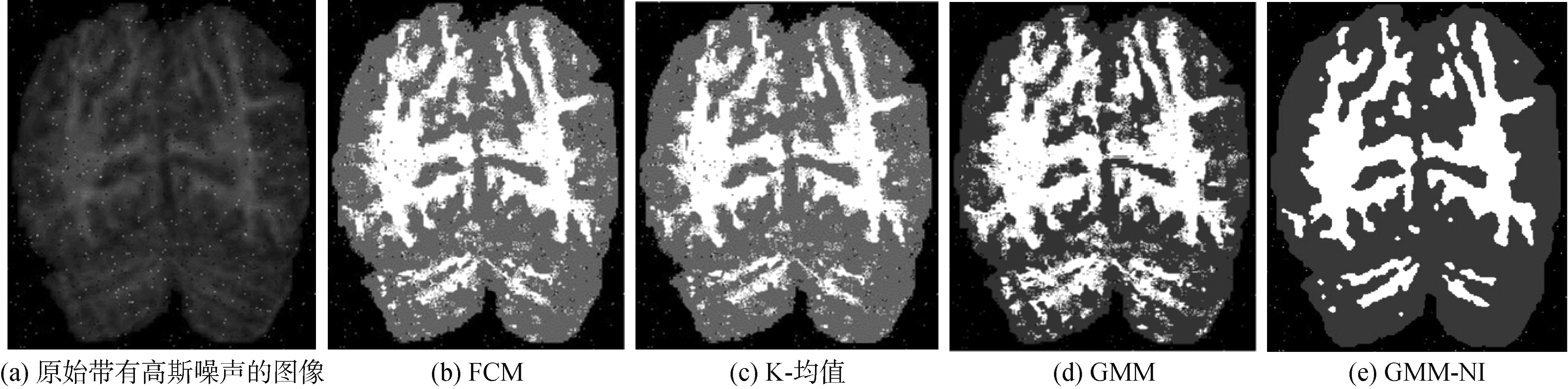
图6 4种算法对含有椒盐噪声的大脑图片的分割结果
Fig.6 Segmentation results on salt&pepper noise images (1%)
从图5、图6可以看出， GMM-NI方法对噪声的平滑处理十分优秀,而FCM、K-均值、GMM算法都无法有效滤除高斯噪声点。
对添加均值为0，方差分别为0.01、0.03、0.05、0.08的高斯噪声和对添加浓度分别为0.005、0.01、0.03、0.05的椒盐噪声的图像进行比较实验，结果见图7、图8。
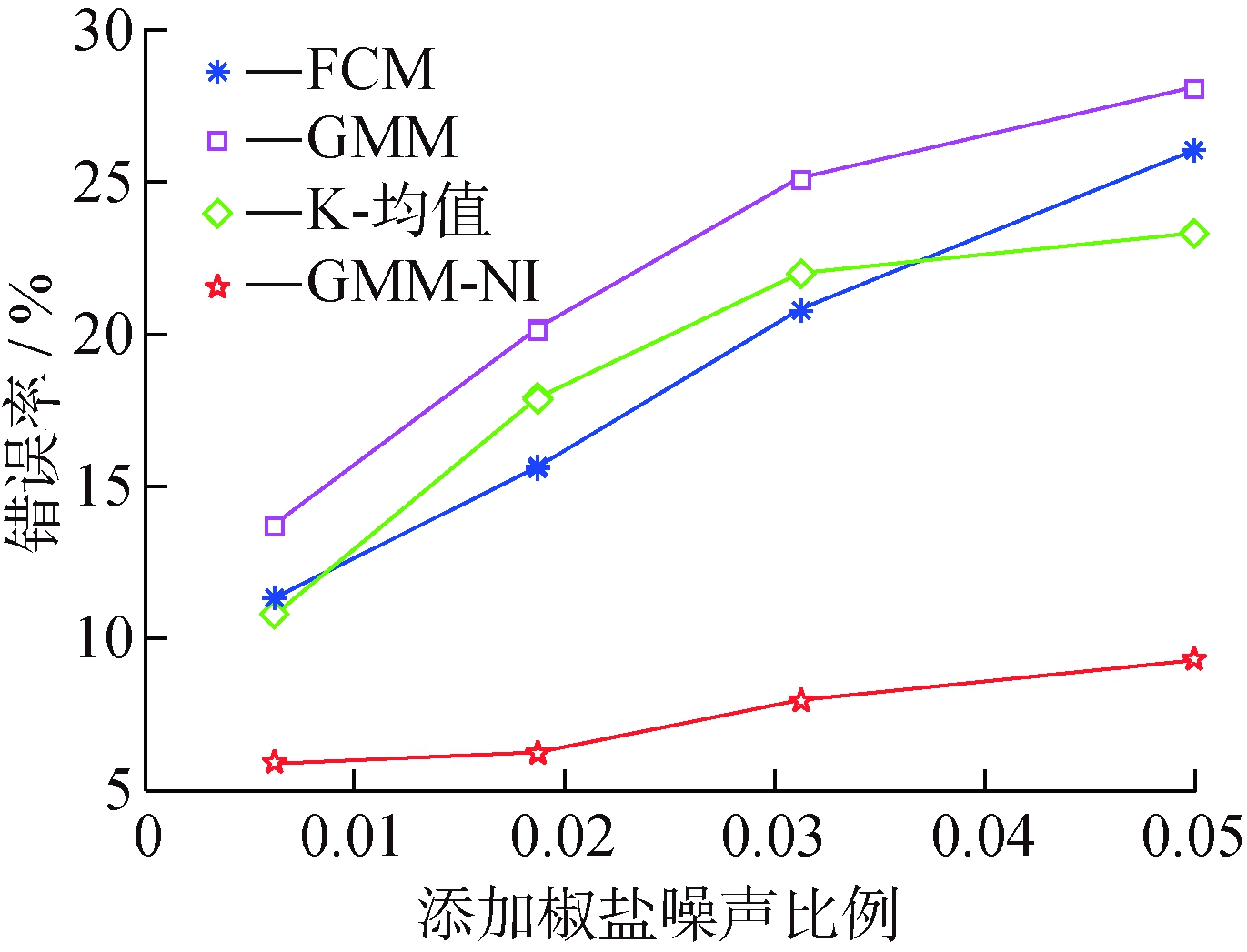
图7 添加高斯噪声后图像分割的错误率
Fig.7 Error rate of the segmentation with Gaussian noise
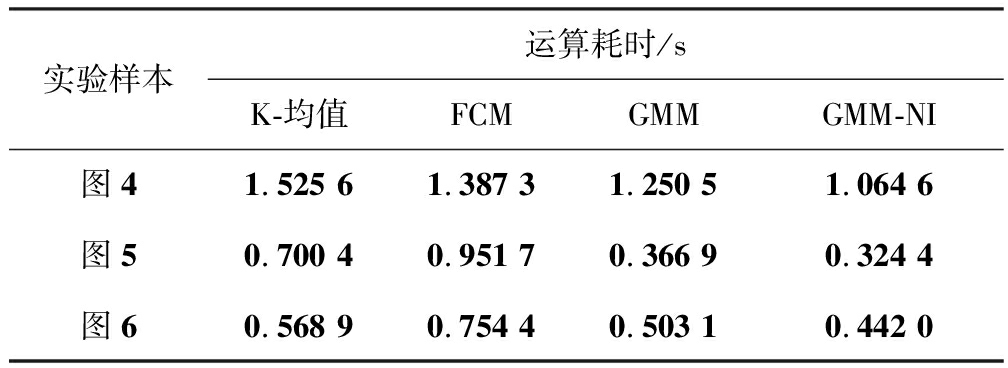
由图7、图8可以看出，本文算法在高斯噪声下的图像分割错误率控制在了10%以下。在含有椒盐噪声图像的分割效果下，对比其他3种方法，本文有极大的效果提升，错误率也在其他算法的一半以下，所以验证了本文提出的聚类分割算法在MRI处理上的优秀性能。通过表2也可以看出，在相同的样本条件下，本文算法在时间复杂度上要优于其他3种算法。尤其与GMM进行对比，结果表明使用梯度法的确比使用EM算法更高效。
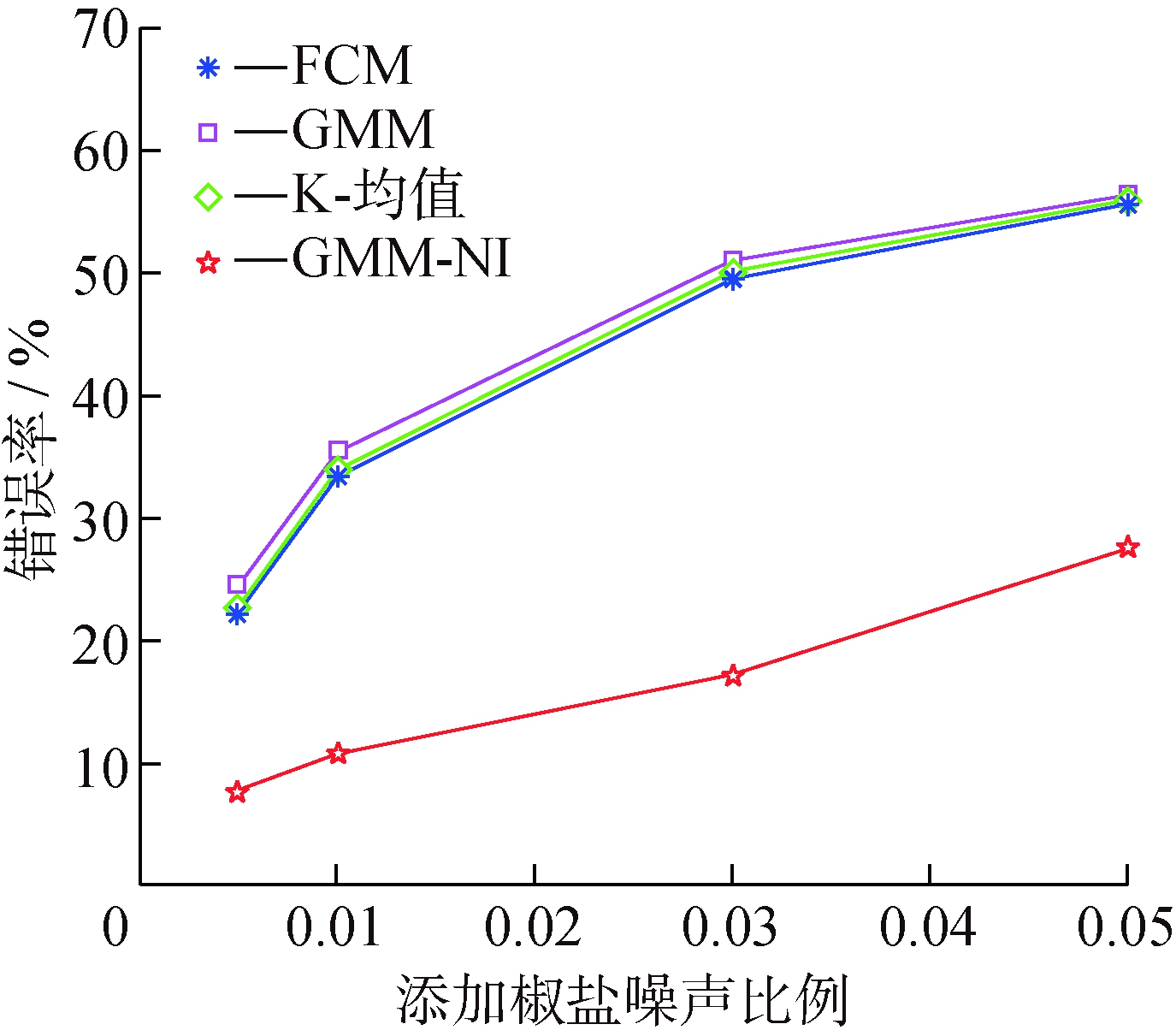
图8 添加椒盐噪声后图像分割的错误率
Fig.8 Error rate of the segmentation with salt & pepper noise
表2 4种算法的运算性能
Table 2Run time of the performances of four algorithms
4结束语
本文提出了一种基于狄利克雷分布和参数分析的高斯混合模型图像分割算法。通过对图像每个像素点求取概率高斯函数的概率值，并使用基于狄利克雷分布的邻域滤波模板进行平滑。然后使用梯度下降法对误差函数进行计算和参数更新，最后根据像素的概率值进行聚类，并分配标记。由于算法使用了基于狄利克雷分布的滤波模板和梯度下降法，所以它对噪声图像有很好的分割效果而且运算复杂度也较小。通过与3种传统图像聚类分割算法的实验结果对比说明本文算法更有优越性。
参考文献：
[1] MCLACHLAN G J, PEEL D. Finite Mixture Models [M] . New York: Wiley,2000.
[2] JAIN A K, DUIN R P W. Statistical pattern recognition: A review[J].IEEE Transactions on Pattem Analysis and Machine InteIligence,2000,22(1):4-37.
[3] REDNER R A, WALKER H F. Mixture densities, maximum likelihood and the EM algorithm[J]. SIAM Review,1984,26(2):195-239.
[4] 刘海华, 郭杰龙. 基于高斯混合模型的腹主动脉图像分割[J].中南民族大学学报(自然科学版),2015,34(2):91-94.
[5] JO
O M, PEREIRA S, SILVA C A,et al. Modelling brain tissues intensities using Dirichlet process[C]//2017IEEE5th Portuguese Meeting on Bioengineering. Portugal: IEEE,2017:1-4.
[6] NGUYEN T M, WU Q M. Robust student’s-t mixture model with spatial constraints and its application in medical image segmentation[J]. IEEE Transactions on Medical Imaging,2012,31(1):103-116.
[7] NIKOU C, LIKAS A C, GALATSANOS N P. A Bayesian framework for image segmentation with spatially varying mixtures[J]. IEEE Transactions on Image Processing,2010,19(9):2278-2289.
[8] DORNA Z, MEHRAN Y. Automatic segmentation of multiple sclerosis lesions in brain MRI using constrained GMM and genetic algorithm[C]//24th Iranian Conference on Electrical Engineering (ICEE).USA: IEEE,2016:832-837
[9] RAGOTHAMAN S, NARASIMHAN S, BASAVARAJ M G,et al. Unsupervised segmentation of cervical cell images using Gaussian mixture model[C]// IEEE Conference on Computer Vision and Pattern Recognition Workshops. USA: IEEE,2016:1374-1379.
[10] ZHANG Y, BRADY M, SMITH S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm[J]. IEEE Transactions on Medical Imaging,2001,20(1):45-57.
[11] PHAM D, PRINCE J L. Adaptive fuzzy segmentation of magnetic resonance images[J]. IEEE Transactions on Medical Imaging,1999,18(9):737-752.
[12] LIEW A W C, YAN H. An adaptive spatial fuzzy clustering algorithm for3-D MR image segmentation [J]. IEEE Transactions on Medical Imaging,2003,22(9):1063-1075.